Vorwissen
Bevor es richtig losgeht noch eine kurze Erinnernung an ein paar wichtige Punkte.
- Es kann nicht mit Punkten sondern nur mit deren Ortsvektoren gerechnet werden.
- Ortsvektoren sind die Pfeile, die vom Ursprung bis zum jeweiligen Punkt gehen.
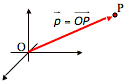
- Ein Punkt und sein Ortsvektor haben die gleichen Koordinaten nur das beim Punkt die Komponenten nebeneinander stehen und beim Vektor übereinander.
P(2|0|4) und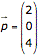
Der Orstvektor hat den gleichen Namen wie sein Zielpunkt nur klein geschrieben.
Eine Anmerkung noch zum ersten Punkt. Es kann durchaus passieren, dass die Trennung zwischen Punkt und Ortsvektor vom Lehrende nicht so exakt von einander getrennt wird. Das kann durchaus sinnvoll sein und macht auch kein Problem. Im wesentlichen geht es eigentlich ja auch nur um das Rechnen mit 3er oder 2er-Tupeln. Und ob die jetzt übereinander oder nebeneinander stehen ist für die mathematische Behandlung unerheblich.
Ich selbst, wie auch viele Kollegen, bestehen auf dem Unterschied. Das liegt daran, dass wir in dem Schüler ein Gefühl für den Unterschied wecken möchten und im Anschaulichen bleiben wollen. Und da ist es einfach ein Unterschied, ob man von einem Punkt oder einem Vektor spricht.
Formelsammlung
Zunächst ein paar Grundlagen im Überblick. Die meisten Dinge sollten klar sein, daher werde ich nicht darauf weiter eingehen. Sollte es dennoch hier bereits hacken, so würde ich das persönliche Gespräch beim Lehrer vorziehen. Gerade bei dem Grundlagen halte ich eine individuelle Betreuung vür am Besten.
Länge eines Vektors
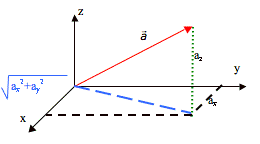
Die Länge eines Vektors ist die Wurzel aus der Summe der Komponentenquadrate:
Die Herleitung dieser ersten Formel ist eigentlich ganz einfach. Und läuft wie folgt ab:
- Die blaue Strecke wird mit Hilfe des Pythagoras berechnet: ax2+ay2 = blaue Strecke2
- az2 + blaue Strecke2 = rote Strecke2
oder ersetzt
az2 + ax2+ay2 = rote Strecke2
Zieht man die Wurzel auf beiden Seiten, so erhält man obige Gleichung.
Jetzt noch ein paar Definition:
Verbindungsvektor
Der Vektor vom Punkt A nach B wird durch 
berechnet (vgl. Subtraktion).
Vektoraddition
Die Vektoren 
und 
werden addiert, in dem sie grafisch aneinandergehängt werden
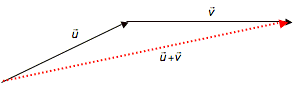
bzw. komponentenweise addiert werden:
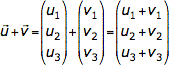
In Realschulen ist es wohl üblich statt dem Plus einen Kreis mit Plus zu schreiben, um die Vektoraddition von der normalen Addition duetlich zu trennen. Daher hier nochmal die "Realschulversion":
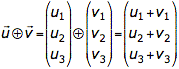
Vektorsubtraktion
Die Vektoren und
werden subtrahiert, in dem die Vektoren im gleichen Punkt beginnen und die Pfeilspitzen miteinander verbunden werden. Dabei zeigt der Ergebnispfeil auf den Minuenden (den erst genannten Vektor):
bzw. komponentenweise subtrahiert werden:
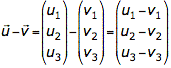
Skalarprodukt 1
Das Skalarprodukt der Vektoren und ist die Summe der Komponentenprodukte:
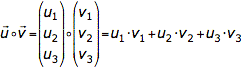
Das Ergebnis ist eine Zahl (Skalar).
Skalarprodukt 2
Das Skalarprodukt der Vektoren und
ließe sich auch wie folgt berechnen:
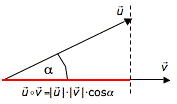
Das Skalarprodukt ist die Länge der Projektion des Vektors auf (hier rot dargestellt).
Und damit die Länge von mal die Länge von multipliziert mit dem Kosinus des eingeschlossenen Winkels.
Auf Grund dieser Definition ist dann auch klar, dass das Skalarprodukt von zwei rechtwinkligen Vektoren 0 ergibt; der Kosinus von 90 Grad ist Null bzw. die Projektion hat keine Länge.
Das Skalarprodukt wird in vielen Beweisen benutzt um die Orthogonalität von Vektoren zu beweisen. Auch der Schnittwinkel von Geraden untereinander und Geraden mit Ebenen etc. kann mit Hilfe des Skalarprodukts berechnet werden.
Kreuzprodukt
Das Kreuzprodukt der Vektoren und
ist eigentlich nichts anderes als die Entwicklung der folgenden Determinante nach der ersten Zeile:
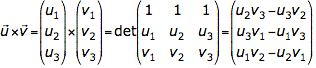
Einfacher zu merken in der folgenden Merkregel:
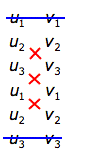
Wobei die Diagonalen non links unten nach rechts oben subtrahiert werden.
Das Ergebnis ist ein Vektor, der senkrecht auf den gegebenen Vektor und
steht und zwar so, dass ein Linkssystem ensteht.
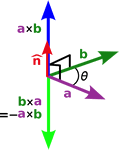
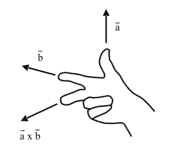Rechte-Hand-Regel
Lineare Abhängigkeit und Basis
Nun zu einem extrem wichtigen Begriff, der, wenn er einmal verstanden wurde, sehr einfach ist, aber leider vielen Problemen macht.
Lineare Abhängigkeit
Vektoren heißen linear abhängig, wenn folgendes gilt:
Sonst heißen sie linear unabhängig.
Mit anderen Worten: Man kann n Vektoren so aneinander hängen, dass man wieder am Ausgangspunkt herauskommt. Dabei darf man die Vektoren dabei länger machen (|ri|>0), kürzer machen (|ri|<1) oder umdrehen (ri<0).
Folgerungen:
Im Zweidimensionalen bedeutet das, dass zwei Vektoren nicht auf einer Geraden liegen dürfen. Im Dreidimensionalen dürfen sie nie in einer Ebene liegen.
Auch kann man weiter folgen, das n+1 viele n-dimensionale Vektoren immer linear abhängig sind. Drei zweidimensionale Vektoren sind genauso immer linear abhägning, wie auch vier dreidimensionale Vektoren.
Umgekehrt kann man auch die Frage stellen, wie viele verschiedene Vektoren benötigt man, um z.B. alle Punkte eines dreidimensionalen Raums zu erreichen?
Verschieden meint hierbei "in verschiedene Richtungen zeigend bzw. unterschiedlich lang sein.
Die Antwort lautet "mindestens 3"; aber 3 Vektoren würden genügen, wenn sie linear abhängig sind. Daher kommt auch der Name "dreidimensional".
"Drei" gibt die Anzahl der Vektoren an und "Dimension" kann vereinfacht als Richtung übersetzen.
Basis
n Vektoren heißen Basis eines n-Vektorraums, wenn sie linear unabhängig sind.
Der Begriff lineare Unabhängigkeit ist deswegen so wichtig, weil alle weiteren Untersuchungen (Geraden-Geraden-Schnitte, Geraden-Ebenen-Schnitt, Ebenen-Ebenen-Schnitt) zunächst auf der Untersuchung auf lineare Abhängigkeit basieren.
Teilen von Strecken
In den meisten Fällen ist das Teilen von Strecken ganz einfach. Ein Punkt T liegt irgendwo auf einer Strecke [AB] und teilt damit die Strecke in zwei Abschnitte [AT] und [BT] ein. Das Verhältnis dieser Strecken ist das Teilungsverhältnis τ (sprich: "Tau"):
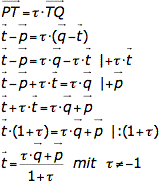
Teil ein Punkt T die Strecke [AB] an einer bestimmten Stelle, so ist das Teilungsverhältnis 
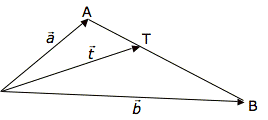
- Innere Teilung: τ ist positiv
- Äußere Teilung: τ ist negativ; für -1<τ<0 liegt der Teilpunkt T außerhalb der Strecke [AB] auf der Seite des Anfangpunkts und für τ<-1 außerhalb auf der Seite des Endpunkts.
Flächen und Rauminhalte
Mit Hilfe der aufspannenden Vektoren lassen sich nun einfach und schnell die wesentlichen Grundfiguren berechnen.Flächeninhalte
Flächeninhalt des Parallelogramms, das von den Vektoren a und b aufgespannt wird:
Flächeninhalt des Dreiecks, das von den Vektoren a und b aufgespannt wird:
Für Dreiecke im R2 erhält man daraus die Formel 
Natürlich gibt es auch für die enstprechenden Körper eine Formel.
Volumen
Volumen des Parallelepipeds, das von den Vektoren a, b und c aufgespannt wird (Spatprodukt):
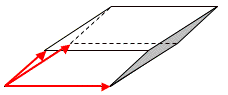
Volumen des Tetraeders, der von den Vektoren a, b und c aufgespannt wird:
Rechner
Verbindungsvektor vom Punkt A zum Punkt B
Einzugeben sind ein Punkt A(x|y|z) und ein Punkt B(x|y|z):
Länge eine Vektors und dessen Normierung
Grundrechenarten mit Vektoren
Einzugeben sind beide Vektoren und die Rechenart:
Lineare Abhängigkeit von 2 Vektoren
Einzugeben sind beide Vektoren
Lineare Abhängigkeit von 3 Vektoren
Einzugeben sind drei Vektoren
Winkel zwischen 2 Vektoren
Einzugeben sind beide Vektoren