Bruchrechnung - Addition und Subtraktion

Wieviel Kuchen muss gekauft werden, wenn insgesamt 6 Kinder ein Stück Apfelkuchen haben wollen (1/12) und 5 Kinder ein Stück Kasekuchen (1/16)? Eine Antwort auf diese Frage würde die folgende Rechnung liefern: 
		 6    5
		-- + -- = ???
		12   16
Aber wie werden solche Aufgaben berechnet? Dazu ein anschaulicheres Beispiel:

1
-
2
 + 
1
-
5
1_2 + 1_5


Einfach nur die Kuchen aneinanderlegen reicht nicht, da das Ergebnis wieder ein Bruch ist und daher die Stücke wieder gleichgroß sein müssen (Nenner!). Man muss also zunächst die Brüche auf den gemeinsamen Nenner bringen, sozusagen beide Teilkuchen in gleichgroße Stücke zerlegen. In obigem Fall ist der gemeinsame Nenner 10, da ich beide Brüche auf den Nenner 10 erweitern kann.

1
-
2
 + 
1
-
5
 = 
5
-
10
 + 
2
-
10
1_2 + 1_5 = 5_10 + 2_10


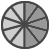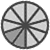Jetzt lassen sich die Stücke einfach aneinanderlegen und die Anzahl der Zehntel sich abzählen:

1
-
2
 + 
1
-
5
 = 
5
-
10
 + 
2
-
10
 = 
7
-
10
1_2 + 1_5 = 5_10 + 2_10 = 7_10


Man muss sich also merken, dass man vor dem Addieren erst gleichgroße Stücke erzeugen muss. Beim Subtrahieren gilt diese Regel selbstverständlich auch, denn nur so lassen sich einfach ein paar Stücke wegnehmen:

1
-
2
 - 
1
-
5
 = 
5
-
10
 - 
2
-
10
 = 
3
-
10
1_2 - 1_5 = 5_10 - 2_10 = 3_10


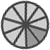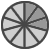Man findet einen gemeinsamen Nenner durch folgenden Überlegung: Der neue Nenner muss die alten Nenner der beiden Brüchen als Teiler enthalten, denn man kann den Vorgang des Erweiterns direkt durch kürzen wieder rückgängig machen. Erinnert man sich an die Primfakorzerlegung einer Zahl, so gilt die Regel: eine Zahl ist genau durch eine andere teilabr, wenn die ursprüngliche in ein Produkt von Zahlen zerlegt werden kann, in der die zweite Zahl mit auftaucht.

Beispiel: 16 = 4 * 4 = 2 * 8 = 2 * 2 * 2 * 2
Somit entsteht ein gemeinsamer Nenner einfach durch multiplizieren der beiden gegebene Nenner. Allerdings entstehen dabei oft sehr große Zahlen. Besser ist es den sogenannten Hauptnenner zu bestimmen.

Definition: Hauptnenner

Der Hauptnenner von den Brüchen z1/n1 und z2/n2 ist das kleinste gemeinsame Vielfache der Nenner, also kgV(n1,n2).


Aufgaben zum Addieren und Subtrahieren von (unechten) Brüchen

Gib zunächst beide Brüche mit dem Hauptnenner an und addiere oder subtrahiere anschließend.

------- -------   =   ------- -------   =   -------




nur positive Zähler im Ergebnis  


Addieren und Subtrahieren von gemischten Brüchen

Das Rechen mit gemischten Brüchen kann je nach Methode unterschiedlich gut geeignet sein. Sowohl bei der Addition als auch bei der Subtraktion bietet es sich jedoch an die gemischten Brüche bei zu behalten.

Definition: Addition gemischter Brüche

Sind zwei Brüche als gemischte Brüche gegeben, so addiert man diese nach folgendem Schema:

1. Die Teilbrüche werden auf den Hauptnenner gebracht.
2. Die ganzen Zahlen werden addiert und die Zähler werden addiert.
3. Aus dem Teilbruch werden eventuell Ganze herausgezogen.
4. Der Teilbruch wird gekürzt.

Natürlich kann man auch die gemischten Brüche erst in unechte Brüche umwandeln und dann wie oben normal addieren.


Beispiel 
		  4     1     16      5     21      1
		1 - + 2 - = 1 -- + 2 -- = 3 -- = 4 --
		  5     4     20     20     20     20


Das Subtrahieren gestaltet sich an einer Stelle, läuft ansonsten genauso.

Definition: Subtrahieren gemischter Brüche

Sind zwei Brüche als gemischte Brüche gegeben, so subtrahiert man diese nach folgendem Schema:

1. Die Teilbrüche werden auf den Hauptnenner gebracht.
2. Ist der Zähler des ersten Bruchs größer als der Zähler des zweiten, so wird beim ersten Bruch ein Ganzes abgezogen und zum Teilbruch addiert.
3. Die ganzen Zahlen werden subtrahiert und die Zähler werden subtrahiert.
4. Aus dem Teilbruch werden eventuell Ganze herausgezogen.
5. Der Teilbruch wird gekürzt.

Natürlich kann man auch die gemischten Brüche erst in unechte Brüche umwandeln und dann wie oben normal addieren.


Beispiel 
		  1     5      5     16  (1)    25     16        9    9
		2 - - 2 - = 2 -- - 1 --   =   1 -- - 1 --  =  0 -- = --
		  4     20    20     20         20     20       20   20

An der Stelle (1) wurde von den 2 Ganzen des ersten Bruchs 1 Ganzes weggenommen, in 20/20 umgewandelt und zum Teilbruch addiert. So können die Zähler problemlos subtrahiert werden.

Aufgaben zum Addieren und Subtrahieren von gemischten Brüchen
-------      -------   =   -------      -------   =   -------


  


nur positive Zähler im Ergebnis