Einführung

Nicht immer werden sich Aufgaben nach den hier dargestellten Formeln direkt lösen lassen. Dann muss man auf die Grundlagen zurückgreifen. Diese sind neben der Fakultät und dem Binomialkoeffizienten das Zählprinzip auch Produktregel genannt.

Definition: Produktregel

Aus k nichtleeren Mengen M1,M2,...,Mk mit n1,n2,...,nk Elementen kann man

n1·n2·...·nk

verschiedene k-Tupel (x1,x2,...,xk), also Kombinationen, mit ni ∈ Mi.

Interpretationen

Beispiel

Aufgabe

Ein Autokennzeichen besteht nach dem Ortskürzel aus 2 Buchstaben und 4 Ziffern, wobei die erste nicht Null sein darf. Wie viele Kennzeichen gibt es?

Lösung

Es gibt 26 Buchstaben, daher: 26·26·9·10·10·10 = 6084000. Da die erste Ziffer nicht 0 sein darf, gibt es hier nur 9 Möglichkeiten.

Viele der hier dargestellten Regeln lassen sich auf das Ziehen von Kugeln aus einer Urne zurückführen. Beim Lösen von Anwendungsaufgaben sollte man daher auch immer versuchen, das Problem auf das Urnenmodell zu reduzieren.

Sollte es mehr um das Verteilen gehen, so muss man sich den Zusammenhang bewusst machen: Das Verteilen von Kugeln auf Urnen ist auffassbar als Ziehen der Urnennummer für die zu verteilenden Kugeln.

Permutation - Anordnung

Permutationen sind eine wichtige Grundlage im Bereich der Kombinatorik, da die Reihenfolge von Ereignissen oft eine Rolle spielt.

Definition: Permutation ohne Wiederholung

Einer Gesamtheit von n verschiedenen Elementen lassen sich auf

n! = n·(n-1)·(n-2)·...·2·1   

Möglichkeiten anordnen. Die Reihenfolge der Elemente muss berücksichtigt werden. Es gilt 0! = 1.

Sprich: "n Fakultät"

Interpretationen

Berechnung

n =n! =

Beispiel 1

Aufgabe

Auf wie viele Arten können sich 3 Menschen hintereinander aufstellen?

Lösung

Der erste hat 3 Plätze zum Hinstellen zur Verfügung, der zweite 2, der Dritte 1 Platz zur Verfügung. Somit sind folgende Permutationen (Vertauschungen) denkbar: (1,2,3), (2,1,3), (2,3,1), (3,1,2), (1,3,2), (3,2,1). Die Anzahl der Möglichkeiten beträgt damit 3! = 3 · 2 · 1 = 6.

Definition: Permutation mit Wiederholung

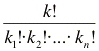
perm_mWdh

mit k1+k2+...+kn = k.

Interpretationen

Beispiel 2

Aufgabe

Auf wieviele Arten kann man die Buchstaben des Wortes "MISSISSIPPI" anordnen, so dass Wörter entstehen?

Lösung

Man kann die 11 Buchstaben auf 11! Möglichkeiten anordnen. Da sich die "S" aber nicht unterscheiden, muss 11! durch die Anzahl der Anordnungen der 4 "S" teilen. Bislang ergibt sich somit 11!/4!. Das Gleiche gilt für die vier "I" und die zwei "P". Insgesamt ergibt sich somit 11!/(2!·4!·4!·1!). Die 1! wurde hinzugenommen, da k1+k2+...+kn = k also 2+4+4+1 = 11 gelten muss. Es ergeben sich 34650 Möglichkeiten.

Auswahl oder Variation

In vielen Fällen werden gar nicht alle Elemente einer Menge angeordnet, sondern nur eine Teilmenge. Ein Beispiel ist die Ziehung der Lottozahlen. Hier werden nur 6 von 49 Zahlen gezogen, wobei die Reihenfolge der Ziehung der Lottozahlen keine Rolle spielt. Ist die Reihenfolge aber entscheidend dann gilt folgende Regel:

Definition: Ziehen ohne Zurücklegen mit Reihenfolge

Einer Gesamtheit von n verschiedenen Elementen kann man

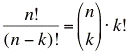
binkoeff

viele Tupel mit k Elementen und Berücksichtigung der Reihenfolge entnehmen, wobei k≤n gilt.

Da n!:(n-k)! = [n·(n-1)·(n-2)·...·1] : [(n-k)·(n-k-1)·...·1] = n·(n-1)·(n-2)·...·(n-k+1) gilt.

Interpretationen

Berechnung

n =, k = Ergebnis =

Beispiel 3

Aufgabe

In einer Urne liegen 10 verschiedene Kugeln beschriftet von 1 bis 10. Aus dieser Urne werden nun nacheinander 3 Kugeln gezogen. Wenn die Reihenfolge nun eine Rolle spielt, also 1,2,3 eine andere Lösung ist als 3,2,1, wieviele Lösungen gibt es?

Lösung

Stellt man sich vor, dass die gezogenene Kugeln in Eierbecher abgelegt werden, so können im ersten Eierbecher 10 verschieden Kugeln liegen. Im zweiten nur noch 9, da eine bereits im ersten Becher liegt. Im dritten und letzten können nur noch 8 verschiedene liegen.

Es ergeben sich: 10·9·8 = 720 Möglichkeiten.

In Bezug auf die Formel ist hier n=10, d.h. man musste rechnen: n·(n-1)·(n-2). Die letzte 2 entspricht k+1, wenn k die Anzahl der zu ziehenden Kugeln ist.

Beispiel 4a

Aufgabe

Ein Flugzeug hat 250 Sitzplätze es sind aber nur 243 Personen an Bord. Wie viele Möglichkeiten für die freie Sitzplätze gibt es?

Lösung

Die Sitzplätze sind von 1 bis 250 durchnummeriert, d.h. man kann sich die Anzahl der Möglichkeiten so überlegen, dass aus einer Urne mit 250 Kugeln sieben gezogen werden. Damit ergeben sich 250 Möglichkeiten für den ersten Platz, 249 für den zweiten etc. Insgesamt also 250·249·248·247·246·245·244 = 56076255733680000. >>

Definition: Ziehen ohne Zurücklegen ohne Reihenfolge (Binomialkoeffizient B(n,k) )

Aus einer Menge von n Elementen lassen sich ohne Berücksichtigung der Reihenfolge

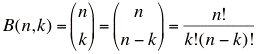
binkoeff

viele Tupel mit k Elementen bilden.

Sprich: "n über k"

Interpretationen

Berechnung

n =, k = Ergebnis =

Im Folgenden soll kurz der Beweis skizziert werden:

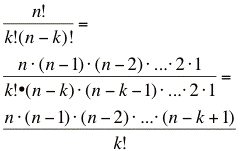
binkoeff

Da man genauso gut die verbleibenden Kugeln untersuchen kann, gilt das erste Gleichheitszeichen.

Beispiel 4b

Jetzt wird nicht mehr in der Reihenfolge unterschieden. Die sieben gezogenen Kugeln lassen sich auf 7! = 5040 Arten anordnen. Denn es ist unerheblich ob der Sitzplatz 137 am Anfang als freier Platz gezogen wird oder am Schluss. Es ergeben sich somit 11126241217000 Möglichkeiten wie die freien Sitzplätze sich verteilen.

Beispiel 5

Auswahl von k=2 elementigen Tupel aus einer Grundmenge {1,2,3,4} mit n=4.

Es ergebn sich 12, 13, 14, 21, 23, 24, 31, 32, 34, 41, 42, 43 zweielementige Tupel ( n!/(n-k)! ), aus denen die Vertauschungsgleichen herausgenommen werden. Da es 2! Möglichkeiten gibt 2 Elemente zu permutieren ergeben sich nur noch 6 Ergebnistupel: 12, 13, 14, 23, 24, 34. Dies entspricht n!/k!(n-k)! .

Eine andere einfache Möglichkeit ist folgendes Szenario: Man hat n=10 Kugeln, k=4 rot, n-k=6 schwarz. Wie viele verschieden Kombination gibt es? Zunächst hat man prinzipiell 10! Möglichkeiten. Davon fallen 4! weg, da die roten Kugeln ja nicht unterschieden werden können. Ebenso fallen 6! Kombinationen weg, da die schwarzen sich auch nicht unterscheiden lassen.

Definition: Ziehen mit Zurücklegen ohne Reihenfolge

Aus einer Menge von n Elementen lassen sich ohne Berücksichtigung der Reihenfolge

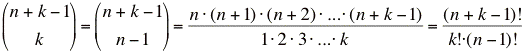
binkoeff

viele Tupel mit k Elementen bilden, wobei die Elemente gleich sein können.

Interpretationen

Berechnung

n =, k = Ergebnis =

Beispiel 6a

Auswahl von k=2 elementigen Tupel aus einer n=4 elementigen Grundmenge.

Ein mögliches Ergebnis sähe so aus: 11, 12, 13, 14, 22, 23, 24, 33, 34, 44 und besteht folglich aus 10 Elementen. Man beachte, dass die zweite Stelle immer größer oder gleich der ersten Stelle ist.

Beispiel 6b

Sechs gleichwertige Ämter sollen auf 20 Schüler verteilt werden, wobei ein Schüler auch mehrere Ämter besitzen kann.

Ein erster Ansatz sähe wie folgt aus: Man legt 20 unterscheidbare Kugeln in eine Urne und zieht mit Zurücklegen (da ein Schüler ja mehrere Ämter haben kann). Der erste Zug ist der Schüler für das erste Amt, der zweite Schüler wird beim zweiten Zug dem zweiten Amt zugeordnet etc. Dennoch ist dieser Ansatz falsch, da die Reihenfolge der Ämter berücksichtigt wird. 1,2,5,2,4,7 (der Schüler mit der Nummer 2 hat also zwei Ämter) wäre ein anderes Ergebnis als 1,5,2,2,4,7.

Richtig wäre es die 6 Ämter auf die 25 Schüler zu verteilen. Die Ämter seine A,B,C,D,E,F und ein Lösung so wie folgt aus:

||A||B,D|||||C||||E|||F|||.

Die senkrechte Striche sollen die Schüler voneinander trennen (man benötigt also 19 Stück. In dem Beispiel hat der dritte Schüler das Amt A, der Schüler mit der Nummer 5 die Ämter B und D usw.

Da es keine Rolle spielen soll, welches Amt jemand ausübt, kann man an Stelle von sechs verschiedenen Buchstaben auch nur A wählen:

||A||A,A|||||A||||A|||A|||

Das wäre dadurch zu realisieren, dass der Name des Amts in einem Briefumschlag steckt, wobei die Umschläge nicht zu unterscheiden sind.

Die Anzahl der Anordnungen dieser Striche und A's entsprechen damit der Anzahl der möglichen Ämterverteilungen wobei die Striche und die A's vertauschbar sind. Das erinnert gleich an den Mississippi-Ansatz. Es sind (20-1)+6 Objekte, die permutiert werden. Wobei man ein Vertauschen der As und der Striche nicht erkennt, daher müssen diese herausgenommen werden.
Man erhält also [(20-1)+6]!/(20-1)!*6!=177.100 . Oder mit n=20 und k=6 die obige allgemeine Formel.

||A||A,A|||||A||||A|||A||| |||||||||||||||||||

Das Ziehen mit Zurücklegen ohne Berücksichtigung darf nicht mit Verwechselt werden mit dem Ziehen mit Zurücklegen unter Berücksichtugung der Reihenfolge. Ein typisches Beispiel ist das Würfeln mit 2 Würfeln. Im ersten Fall gibt es nur 21 Möglichkeiten. Wenn man aber die Unterscheidung (1,2)≠(2,1) zu lässt, erhält man 36 Möglichkeiten.

Definition: Ziehen mit Zurücklegen mit Reihenfolge

Aus einer Menge von n Elementen lassen sich unter Berücksichtigung der Reihenfolge

nk

viele Tupel mit k Elementen bilden, wobei die Elemente gleich sein können.

Interpretationen

Berechnung

n =, k = Ergebnis =

Beispiel 7

Auswahl von k=2 elementigen Tupel aus einer n=4 elementigen Grundmenge und der Unterscheidung bzgl der Reihenfolge.

Das Ergebnis lautet: 11, 12, 13, 14, 21, 22, 23, 24, 31, 32, 33, 34, 41, 42, 43, 44 und besteht folglich aus 16 Elementen. Hier durchläuft sowohl die erste Stelle die Werte 1 bis 4 als auch die zweite Stelle.

Formelsammlung

mit Reihenfolgeohne Reihenfolge
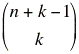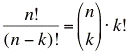mit Wiederholungnkbinkoeff
ohne Wiederholungbinkoeffbinkoeff

Rechner

n = , k =
mit Reihenfolgeohne Reihenfolge
mit Wiederholung
ohne Wiederholung

Beispiele

Für die Beispiele wurde n=4 und k=2 gewählt.

mit Reihenfolgeohne Reihenfolge
mit Wiederholung11, 12, 13, 14,
21, 22, 23, 24,
31, 32, 33, 34,
41, 42, 43, 44
Alle denkbaren Kombinationen:
16 Elemente		11, 12, 13, 14,
22, 23, 24,
33, 34,
44
Alle Permutationsdoppelten wie z.B.
(1,2), (2,1) werden weggenommen:
10 Elemente
ohne Wiederholung12, 13, 14,
21, 23, 24,
31, 32, 34,
41, 42, 43
Die Diagonale wird weggenommen:
12 Elemente		12, 13, 14,
23, 24,
34
Die Permutationsdoppelten und
die Diagonale wird rausgenommen:
6 Elemente

Aufgaben mit Lösungen

Aufgabe 1

a) Berechnen Sie die Anzahl der 3-Tupel aus {1,2,3,4}.

b) Berechnen Sie die Anzahl der 3-Tupel aus {1,2,3,4}, die mit 2 beginnen.

Lösung von Aufgabe 1

Aufgabe 2

Wie können sich 10 Vögel auf 5 Bäume verteilen?

Lösung von Aufgabe 2

Aufgabe 3

In der Schifffahrt gibt es das Winkeralphabet. Eine Art Morsealphabet mit Flaggen. Für den rechten Arm gibt es 7 Positionen. Wie viele muss es für den linken Arm geben, damit alle 26 Buchstaben des Alphabets angezeigt werden können?

Lösung von Aufgabe 3

Links