Die Grund sich mit Wahrscheinlichkeitsrechnung zu beschäftigen liegt in dem Wunsch Ereignisse vorausszusagen. Zu Anfang kam die Motivation aus dem Bereich des Glückspiels. So haben sich viele hochrangige Mathematiker damit beschäftigt vorauszusagen, wie wahrscheinlich bestimmte Ereignisse eines Glückspiels meist Würfelspiels sind.
Definition: Zufallsexperiment
Ein Zufallsexperiment ist eine Experiment, dessen Ausgang nicht vorhersagbar ist (Wüfeln, Roulette, Ziehen von Kugeln aus einer Urne).
Die N Ausgänge eines Zufallsexperiment fasst man in der Ergebnismenge Ω={ωi mit i∈{1,...,N}} zusammen. Beim Würfeln ist Ω={1,2,3,4,5,6} und die Mächtigkeit von Ω, also die Anzahl der Elemente |Ω| = 6.
Meist ist jedoch nicht die Menge der Ergebnisse interessant sonder die Ereignismenge. Diese Menge ist immer mächtiger oder gleich der Menge Ω. Als Beispiel könnte man hier nennen: MEreignis={{1};{2};{3};{4};{5};{6};{1,3,5};{2,4,6};...}.
- Elementarereignis: Die Ereignisse {1},{2},{3},{4},{5} und {6} nennt man Elementarereignis, da sie identisch mit den möglichen Ausgängen des Experiments sind.
- Sicheres Ereignis: Ω, da das Experiment ja immer enden muss.
Unmögliches Ereignis: Ω = ∅
Im Beispiel wird das Würfelergebnis unterteilt in die Ereignisse ungerade Augenzahl vs. gerade Augenzahl.
Beim Einstieg in dieses Thema weiß man oft nicht wo anfangen. Erarbeiten lässt sich das Thema am schnellsten am Beispiel des Würfelns. Hier lässt sich ein Zufallsexperiment durchführen, auswerten und eventuell eine Voraussage machen.
Experiment
Aufgabe
Nehmen Sie ein Legosteinchen mit 8 Noppen und werfe Sie ihn mehrfach.
Lösung
Ω={kleine Seite 1,kleine Seite 2, mittlere Seite 1, mittlere Seite 2, große Seite 1, große Seite 2}. MEreignis={kleine Seite, mittlere Seite, große Seite}
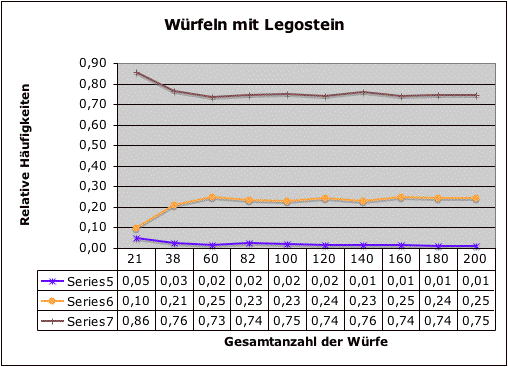
Dargestellt sind relative Häufigkeiten, also die prozentualen Anteile eines Ereignisses in Bezug auf alle möglichen Ereignisse.
Definition: Relative Häufigkeit
Ein Zufallsexperiment liefert k mögliche Ergebnisse. Jedes Ereignis Ai tritt mit der absoluten Häufigkeit n1, n2,...,ni,...,nk auf. Es gilt
| Hn(Ai) = | Anzahl des gewünschten Ereignisses Ai | = | nAi |
| Anzahl aller Ereignisse K | n |
mit i ∈ {1,..,k}.
Axiome
- 0 ≤ Hn(A) ≤1
Die relativen Häufigkeiten sind Werte zwischen Null und Eins. - Hn(Ω) = 1
Das Zufallsexperiment endet immer (1=100%) mit einem Element aus der Ergebnismenge. - Hn(A∪B) = Hn(A) + Hn(B), wenn A∩B = ∅
Die relative Gesamthäufigkeit zweier Ereignisse die nicht gleichzeitig eintreten können, ist die Summe der Teilhäufigkeit.
Wie verteilt man nun die Augenzahlen 1 bis 6 auf die Seiten, so dass man möglichst oft eine 6 würfelt? Jedem wird klar sein, dass man die 6 auf die großen Flächen schreibt, da dieses Ereignis am "wahrscheinlichsten" ist. Aber wie wahrscheinlich? An der relativen Häufigkeit lässt sich ablesen, dass der Stein in ungefähr 75% der Fälle auf der großen Seite liegen bleibt. Da sich dieser Wert über ein doch ziemlich große Anzahl von Würfen eingestellt hat, liegt nahe zu vermuten, dass dies so bleiben wird. Damit ist die Wahrscheinlichkeit also ebenfalls 75%.
Definition: Wahrscheinlichkeit P
Die Wahrscheinlichkeit P (engl.: probability) für das Eintreten des Ereignisses A ist der Grenzwert der relativen Häufigkeiten für viele Durchführungen:
| P(A) = | lim | Hn(A) |
| n→∞ |
Kolmogorov-Axiome
Da die Wahrscheinlichkeit der Grenzwert der relativen Häufigkeiten ist, werden die Axiome übernommen. Dieser Ansatz geht auf den russischen Mathematiker Kolmogorov (1903-1987, veröffentlicht 1933) zurück, weswegen diese Axiome Kolmogorov-Axiome heißen.
- 0 ≤ P(A) ≤1
Die Wahrscheinlichkeit ist ein Wert zwischen Null und Eins. (A1) - P(Ω) = 1
Das Zufallsexperiment endet immer (1=100%) mit einem Element aus der Ergebnismenge. Da ist das Ergebnis dass ein Spielwürfel "brennt" kein gültiges Ergebnis und das Experiment muss wiederholt werden. (A2) - P(A∪B) = P(A) + P(B), wenn A∩B = ∅
Die relative Gesamthäufigkeit zweier Ereignisse die nicht gleichzeitig eintreten können, ist die Summe der Teilhäufigkeit. (A3)
Es ergeben sich folgende Folgerungen:
- P(∅) = 0;
Dies ist eine sehr wichtige Formel, da sich viele Wahrscheinlichkeiten leichter über das Gegenereignis errechnen lassen. Erkennbar sind solche Aufgaben oft an Formelierungen wie beispielsweise "mindestens", "höchstens", etc.P( A ) = 1 - P(A) - P(A)≤P(B), wenn A⊆B.
- P(A∪B) = P(A) + P(B) - P(A∩B)
Die Wahrscheinlichkeit, dass sowohl das Ereignis A als auch das Ereignis B eintritt, ist die Summe der Einzelwahrscheinlichkeiten. Überschneiden sich die Ereignisse, so ist die Wahrscheinlichekit der Schnittmenge wieder zu entfernen.
Die Wahrscheinlichkeit ist nun als Grenzwert der relativen Häufigkeit definiert worden. Eine anderer Ansatz wäre die Wahrscheinlichkeit als Zuordnung aufzufassen. Jedem Elementarereignis A wird eine Zahl zwischen 0 und 1 zugeordnet und P(A) genannt.
Möchte man nun, ohne viele Versuche durchführen zu müssen, die Wahrscheinlichkeit eines Ereignisses berechnen, so merkt man schnell, dass sowohl der erste als auch der zweite Ansatz nicht zum Ziel führen. Weder die Flächengröße, noch der Flächenabstand zum Schwerpunkt o.ä. führen zum Ziel. Glücklicherweise ist dies selten der Fall.
In vielen Fällen, beispielsweise beim Spielwürfel, ist die Wahrscheinlichkeit so, dass jedes Elementarereigniss gleichwahrscheinlich ist. Beim Würfel ist dies 1/6. Die relativen Häufigkeiten streben ja auch gegen diesen Wert, wie man sich durch ein entsprechendes Experiment leicht nachprüft. Daher wird zunächst folgende Vereinfachung getroffen:
Definition: Laplace-Experiment
Sind alle N Elementarereignisse ωi eines Experiments gleichwahrscheinlich, so gilt:
| P({ωi}) = | 1 | für i∈{1,...,N}. |
| N |
Für ein beliebiges Ereignis A gilt:
| P(A) = | Anzahl der für A günstigen Elementarereignisse ωi | = | |A| |
| Anzahl aller Elementarereignisse | |Ω| |
Zusammen mit dem Kolmogorov-Axiom 2 P(Ω) = 1 muss sich die Gesamtwahrscheinlichkeit 1 gleichmäßig auf alle Wahrscheinlichkeiten verteilen.
Definition: Gleichverteilung
Sind alle N Elementarereignisse ωi eines Experiments gleichwahrscheinlich, so spricht man von einer Gleichverteilung der Wahrscheinlichkeit.
Ist man nun in einem konkreten Fall an einer Wahrscheinlichkeit interessiert, so muss die Anzahl der geünschten Ereignisse durch die Gesamtanzahl der möglichen Ausgänge geteilt werden. Damit verlagert sich das Problem eigentlich immer auf den Bereich der Kombinatorik.
Beim Einstieg in das Gebiet der Wahrscheinlichkeitsrechnung stehen viele Schüler vor der Frage: Wann muss man den Wahrscheinlichkeiten addieren und wann multiplizieren? Hierzu zunächst ein Beispiel aus der Kombinatorik.
Beispiel: Morsealphabet
Aufgabe
Das Morsealphabet besteht aus mindestens 1 und maximal 5 Zeichen, wobei jedes Zeichen ein Punkt oder ein Strich sein kann. Wie viele Zeichen können gebildet werden?
Lösung
- 1-stellige Morsezeichen: 2 Möglichkeiten
- 2-stellige Morsezeichen: 2 Möglichkeiten für die erste Stelle und anschließend 2 Möglichkeiten für das zweite Zeichen. Insgesmt ergeben sich somit
2·2=4 Möglichkeiten.
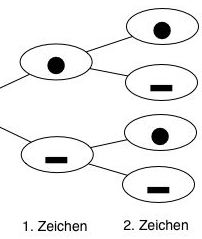
- ...
- 5-stellige Morsezeichen: 25 = 32 Möglichkeiten.
Innerhalb der Bäume mussten also die Möglichkeiten multipliziert werden. Die Gesamtanzahl an Möglichkeiten ergeben sich jetzt durch Addition der Bäume: 21+22+23+24+25 = 62. Damit ergibt sich beispielsweise als P("3-stelliges Zeichen")=23:62≈13%.
Die Überlegung aus dem Beispiel lässt sich auch auf Wahrscheinlichkeiten übertragen. Typisch sind dabei mehrstufige Zufallsexperimente der folgenden Art:
Ziehen mit Zurücklegen
Aufgabe
In einer Urne sind 3 weiße und 1 rote Kugel. Wie wahrscheinlich ist es zwei weiße Kugeln nacheinander mit zurücklegen zu ziehen?
Lösung
Zunächst liegt ein Laplace-Experiment vor,d.h. dass jede Kugel gleichwahrscheinlich ist. Gemäß dem Diagramm gibt es (bei Unterscheidung der
Kugeln) 16 mögliche Ergebnisse:
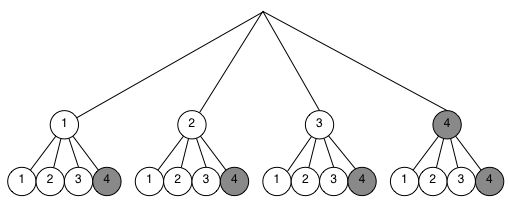
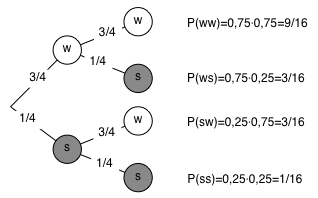
Ein anderer und manchmal natürlicherer Ansatz ist die Überlegung über die Einzelwahrscheinlichkeiten. Für eine weiße Kugel im ersten Zug ist die
Wahrscheinlichkeit 3 von 4, also 3:4=0,75. Im zweiten Zug auf Grund des Zurücklegens ebenfalls. Multipliziert man diese Wahrscheinlichkeit, so erhält man
wiederum 9/16.
Eine andere Möglichkeit wäre über den Binomialkoeffizienten: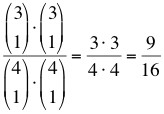
Satz: Pfadregel
Im Baumdiagramm ist die Wahrscheinlichkeit eines Pfades gleichem dem Produkt der Wahrscheinlichkeiten auf den Teilstrecken.
Beachte
- Mit Hilfe dieses Satzes lassen sich ein Vielzahl von mehrstufigen Zufallsexperimente schnell untersuchen.
- Die Ereignisse müssen unabhängig voneinander sein (beim Ziehen ohne Zurücklegen sind die Ereignisse nicht voneinander unabhängig, da sich nach dem ersten Ziehen die Ausganssituation geändert hat).
- Diesen Satz nennt man auch den speziellen Multiplikationssatz.
Aufgabe: Lotto
a) Wie hoch ist die Wahrscheinlichkeit für einen Sechser im Lotto?
b) Wie hoch ist die Wahrscheinlichkeit für "4 Richtige" im Lotto?
Lösung
Aufgabe: Spielende Kinder
Angenommen, Sie fahren am frühen Nachmittag mit dem Auto durch eine ruhige Wohnstraße. Um diese Tageszeit spielen viele Kinder im Freien, und mit einer Wahrscheinlichkeit von 0.01 (1%) rollt ihnen beim Durchfahren der Straße ein Ball vor das Auto. Da leider Kinder noch ein recht unvorsichtiges Verhalten im Straßenverkehr haben, achtet nur eins von Hundert beim Ballholen auf fahrende Autos.
Lösung
Links
- Mathe-Prisma
Bedingte Wahrscheinlichkeit, Multiplikationssatz, Satz von der totalen Wahrscheinlichkeit, Bayessche Formel - Mathe-Prisma
Grundlagen, Pfadregel, Markoff-Ketten